PLANAR GRAPH

 In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other.^[1][2] Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.

Every graph that can be drawn on a plane can be drawn on the sphere as well, and vice versa, by means of stereographic projection.

Plane graphs can be encoded by combinatorial maps or rotation systems.

An equivalence class of topologically equivalent drawings on the sphere, usually with additional assumptions such as the absence of isthmuses, is called a planar map. Although a plane graph has an external or unbounded face, none of the faces of a planar map has a particular status.

Planar graphs generalize to graphs drawable on a surface of a given genus. In this terminology, planar graphs have genus 0, since the plane (and the sphere) are surfaces of genus 0. See "graph embedding" for other related topics.

Planarity criteria[edit]

Kuratowski's and Wagner's theorems[edit]

Proof without words that a hypercube graph is non-planar using Kuratowski's or Wagner's theorems and finding either K₅ (top) or K_3,3 (bottom) subgraphs

The Polish mathematician Kazimierz Kuratowski provided a characterization of planar graphs in terms of forbidden graphs, now known as Kuratowski's theorem:

A finite graph is planar if and only if it does not contain a subgraph that is a subdivision of the complete graph K₅ or the complete bipartite graph K_3,3 (utility graph).

A subdivision of a graph results from inserting vertices into edges (for example, changing an edge • —— • to • — • — • ) zero or more times.

An example of a graph with no K₅ or K_3,3 subgraph. However, it contains a subdivision of K_3,3 and is therefore non-planar.

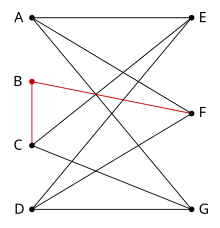
Instead of considering subdivisions, Wagner's theorem deals with minors:

A finite graph is planar if and only if it does not have K₅ or K_3,3 as a minor.

A minor of a graph results from taking a subgraph and repeatedly contracting an edge into a vertex, with each neighbor of the original end-vertices becoming a neighbor of the new vertex.

An animation showing that the Petersen graph contains a minor isomorphic to the K_3,3 graph, and is therefore non-planar

Klaus Wagner asked more generally whether any minor-closed class of graphs is determined by a finite set of "forbidden minors". This is now the Robertson–Seymour theorem, proved in a long series of papers. In the language of this theorem, K₅ and K_3,3 are the forbidden minors for the class of finite planar graphs.

Other criteria[edit]

In practice, it is difficult to use Kuratowski's criterion to quickly decide whether a given graph is planar. However, there exist fast algorithms for this problem: for a graph with n vertices, it is possible to determine in time O(n) (linear time) whether the graph may be planar or not (see planarity testing).

For a simple, connected, planar graph with v vertices and e edges and f faces, the following simple conditions hold for v ≥ 3:

• Theorem 1. e ≤ 3v – 6;
• Theorem 2. If there are no cycles of length 3, then e ≤ 2v – 4.
• Theorem 3. f ≤ 2v – 4.

In this sense, planar graphs are sparse graphs, in that they have only O(v) edges, asymptotically smaller than the maximum O(v²). The graph K_3,3, for example, has 6 vertices, 9 edges, and no cycles of length 3. Therefore, by Theorem 2, it cannot be planar. These theorems provide necessary conditions for planarity that are not sufficient conditions, and therefore can only be used to prove a graph is not planar, not that it is planar. If both theorem 1 and 2 fail, other methods may be used.

• Whitney's planarity criterion gives a characterization based on the existence of an algebraic dual;
• Mac Lane's planarity criterion gives an algebraic characterization of finite planar graphs, via their cycle spaces;
• The Fraysseix–Rosenstiehl planarity criterion gives a characterization based on the existence of a bipartition of the cotree edges of a depth-first search tree. It is central to the left-right planarity testing algorithm;
• Schnyder's theorem gives a characterization of planarity in terms of partial order dimension;
• Colin de Verdière's planarity criterion gives a characterization based on the maximum multiplicity of the second eigenvalue of certain Schrödinger operators defined by the graph.
• The Hanani–Tutte theorem states that a graph is planar if and only if it has a drawing in which each independent pair of edges crosses an even number of times; it can be used to characterize the planar graphs via a system of equations modulo 2.